精子生于 1995 年,英文 ID jysperm.
GPG 与端到端加密:论什么才是可以信任的
本文由我去年 6 月在 LeanCloud 的一次技术分享整理而来,需要读者对公钥加密算法有基本的了解。
如果提到 GPG 那么不得不提的就是公钥加密算法,首先我们先来快速地了解一下最知名的公钥加密算法 —— RSA:在 RSA 中有「公钥」和「私钥」两种密钥,其中私钥可以导出公钥,但公钥无法反推私钥。如果用公钥加密数据的话,那么只有私钥可以解密;如果使用私钥签名数据的话,那么可以验签名。
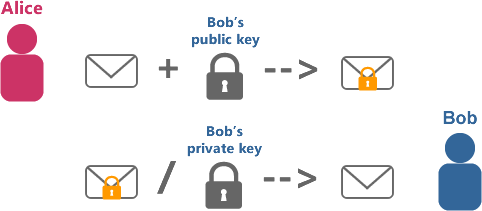
密码学账户
顾名思义,通常我们会将公钥公开地发布,作为自己身份的代表,就好像用户名一样(虽然是一个难以记忆的随机字符串);而将私钥秘密地保存,作为身份的证明,就像密码一样。如果一个账户是由一个公钥加密算法的密钥对所保护的,那我们称之为「密码学账户」,我们身边常见的密码学账户包括:
- SSL 证书(用于 HTTPS 等加密通讯)
- S/MIME 证书(用于邮件加密和认证)
- SSH 密钥(用于登录服务器的凭证)
- Bitcoin 钱包
- GPG ID
这些账户和我们通常注册的互联网服务很不一样,在我们通常注册的互联网服务中,你的账户实际上是由网站的维护者管理的,你为账户设置的密码并没有真的用来加密数据,而只是一种证明账户所有权的凭证,在每次登录时你向网站发送密码,来证明自己是账户的所有者。一旦你忘记了密码,网站的维护者在通过其他渠道(邮箱地址、手机号码)确认了你的身份之后,也可以帮助你重置密码。
而在密码学账户中,你拥有账户的唯一凭证就是你的密钥对 —— 通常是计算机上的一个文件,你通过使用这个密钥对进行签名来管理你的账户、进行解密来访问机密数据。密码学账户既是更加安全的(不存在具有特权的管理者),同时也是更加危险的(一旦丢失无法找回;一旦泄漏也无法重置)。
公钥交换
公钥加密算法看上去很美好,一旦我们有了对方的公钥,只需在通讯时用对方的公钥加密数据,就万无一失了,但这其中 最薄弱的一个环节就是「得到对方的公钥」,即「公钥交换」。

上图是理想的情况,A 和 B 互相之间交换公钥,后续的通讯就可以以加密的方式进行了。但如果这时出现了一个能够监听和篡改 A 和 B 之间的通讯的 C,然后将自己的公钥发给 A 和 B,就变成了这样:
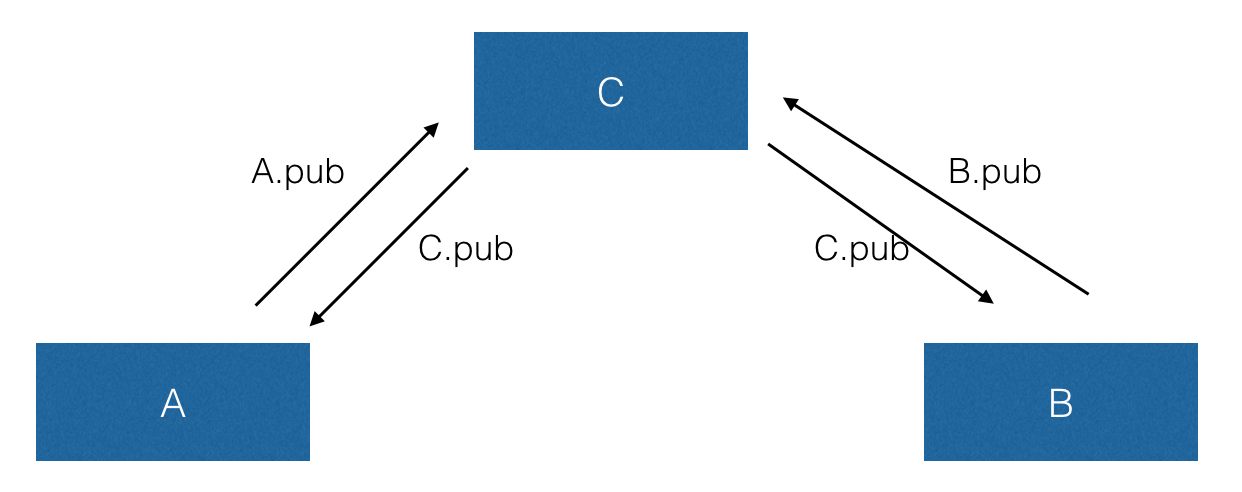
A 和 B 都以为自己得到了对方的公钥,但实际上他们得到的都是中间人 C 的公钥,这意味着他们之后的通讯都会以 C 的公钥来加密,C 便可以在中间继续进行窃听和篡改。
所以在理论上 不可能存在一种在线的、可靠的、不事先协商的公钥交换机制,因为交换公钥意味着双方还没有开始加密通讯,交换的过程自然没有保障。那么在实际应用中我们是如何解决公钥交换的问题的呢,我们来看一下 SSL 所使用的 X.509 证书体系:
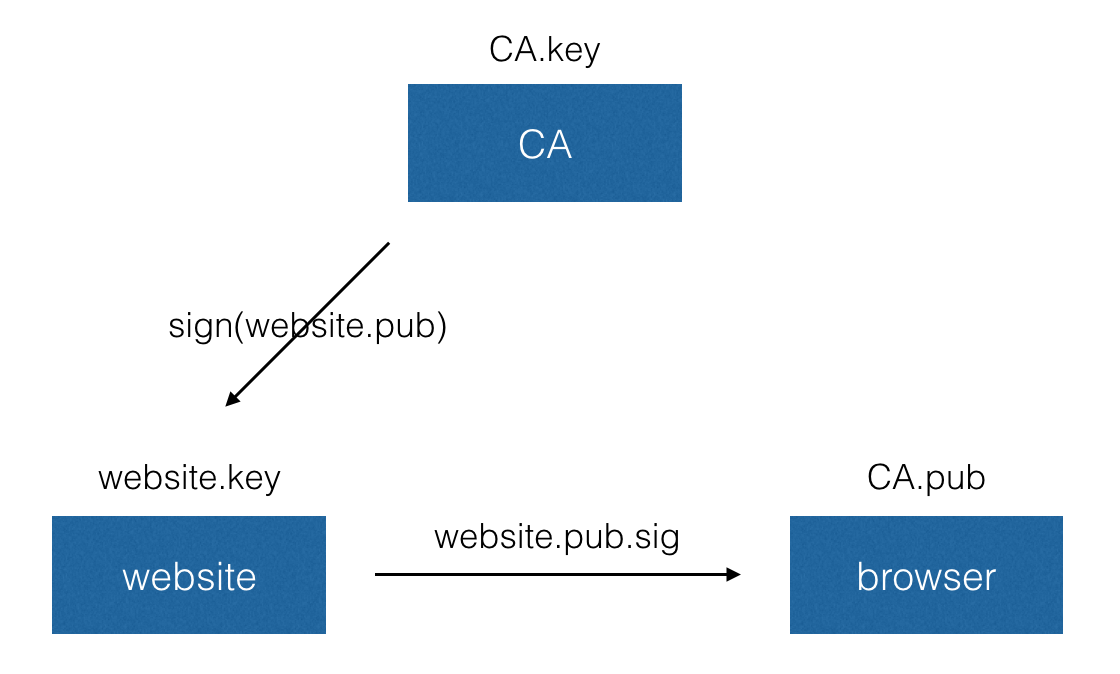
在 X.509 中有一个被称为「证书颁发机构(CA)」的权威的第三方,CA 的数量较为有限,资格变化也并不频繁,所有浏览器(browser)都内置了 CA 的公钥。而网站方(website)在生成了自己的公钥后,需要先找 CA 对自己的公钥进行签名然后才能使用。当浏览器访问一个新的网站时,网站方需要提供经过 CA 签名的公钥,浏览器使用内置的 CA 公钥来验证签名,确保收到的网站的公钥没有被篡改过。
X.509 实际上就是要求大家信任一个权威的第三方并将它们的公钥内置在客户端中,这并不是一个完美的方案,因为在这个体系中 CA 有着非常大的权力,一旦 CA 不按照规则签发证书,那么客户端是无法察觉这种攻击行为的。
GPG
GPG 是 PGP(Pretty Good Privacy)的一个 GPL 实现,也是目前使用最广泛的实现。
「信任一个权威的第三方」对于一些去中心化爱好者是无法接受的:首先我们凭什么去信任这个第三方,其次在 CA 申领证书通常也是需要付费的。那么有没有可能去除这个权威的第三方,而允许大家互相进行认证呢?如何确认一个公钥就是属于这个人的呢?这就是我们接下来要介绍的 GPG 的信任模型:
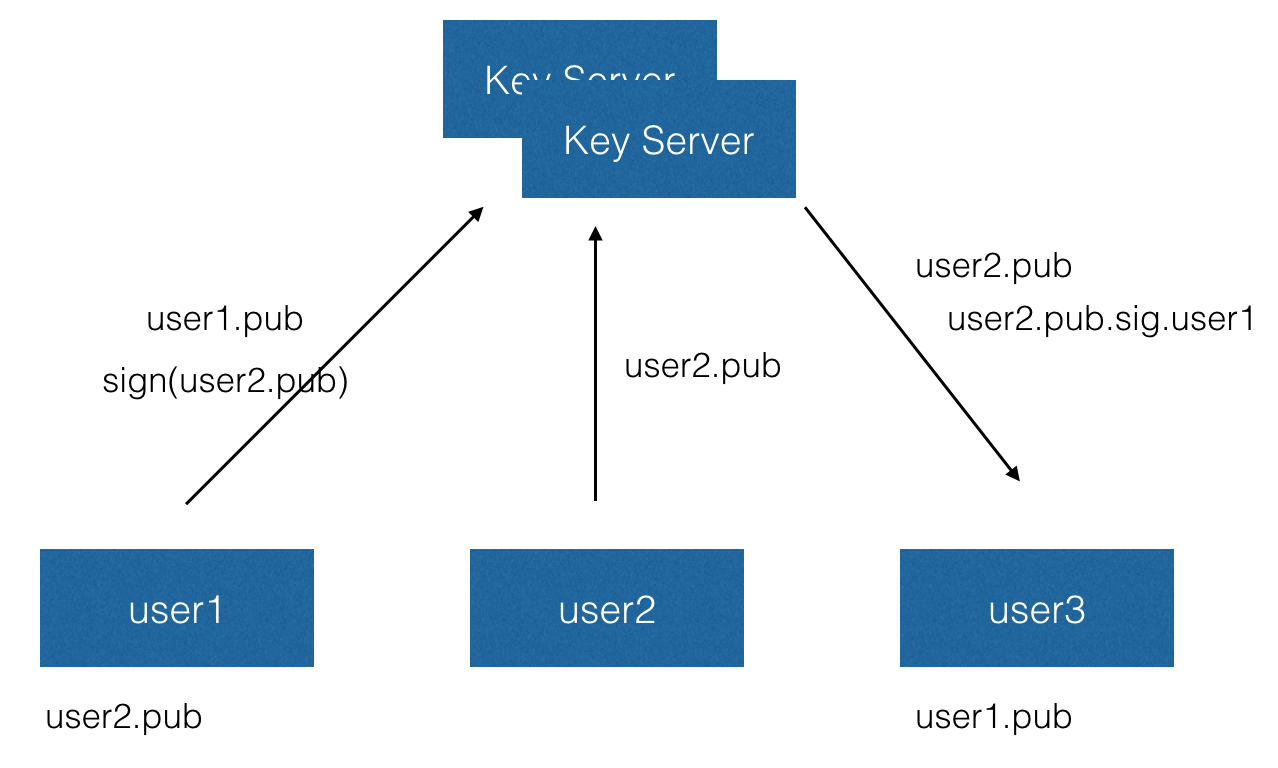
在 GPG 的信任模型中,用户互相之间对公钥进行认证(通过用自己的私钥进行签名的方式),例如 Alice 和 Bob 是很好的朋友,要么 Alice 就会用自己私钥给 Bob 的公钥签名,然后将这个签名通过 Key Server 广播给其他人。Key Server 仅仅用来交换公钥和签名,因为签名本身是可校验的,所以 Key Server 并没有任何特权。
当另外一个 Alice 的朋友看到 Bob 的公钥,并且发现 Alice 给 Bob 的公钥签过名,那么就可以认为他的朋友 Alice 已经检查过 Bob 的公钥了,如果看到更多朋友给 Bob 签过名,那么就几乎可以认定 Bob 的身份是真实的。
所以 GPG 实际上是一个由「熟人关系」建立起的信任网络,当你认可一个人的身份,即认可这个公钥是属于这个人的,你便可以给他的公钥进行签名,形成一种信任关系,同时这种信任关系又是可以传递的。当你的 GPG 通讯录中有了一些互相信任的朋友之后,便可基于这个关系网来拓展你的朋友圈。
那么既然我们前面提到不可能有一个在线的、可靠的、不事先协商的公钥交换机制,那么这个信任网络在一开始是如何建立起来的呢?答案是使用分散的、多渠道的、可能是线下的方式来交换和确认公钥。如果使用一个固定的协议去交换公钥,而且这个协议本身没有加密保护,那么当然容易被中间人攻击,但如果两个人同时使用多种渠道来交换公钥,例如先用邮件发一次、再用微信发一次、最后再用电话说一次,那么这些渠道同时被攻击的可能性会非常小。
或者更进一步,我们可以采用线下的方式来进行确认,实际上很多技术类会议结束后可能会有一个 Key Signing Party 的活动,大家面对面地确认身份(你可能有必要出示印有照片的证件,例如身份证或护照),用纸和笔记下公钥,然后回家进行签名和上传。

最后你便得到了一些来自其他人签名,代表他们认可了你的身份,即认可了某一个 GPG 公钥代表了你。
GPG 通讯簿
因为 GPG 需要用户自己维护信任关系,因此每个 GPG 的用户都会有一个通讯簿,里面是大量的公钥(代表着一个其他用户)和签名(代表着信任关系)。
下面是我的通讯录中与我自己相关的部分:
~> gpg --list-keys jysperm
pub 4096R/E466CF1E 2014-11-23 [expires: 2017-05-17]
uid [ultimate] Wang Ziting <jysperm@gmail.com>
uid [ultimate] Wang Ziting <jysperm@icloud.com>
uid [ultimate] [jpeg image of size 1476]
sub 2048R/1D795875 2014-11-23 [expires: 2017-05-17]
sub 2048R/289286B3 2014-11-23 [expires: 2017-05-17]
sub 2048R/35B5DE4D 2016-05-17 [expires: 2017-05-17]
其中 E466CF1E 是我的「根公钥」的简写形式,4096R 表示这是一个 4096 bit 的 RSA 密钥对,创建时间是 2014-11-23,有效期至 2017-05-17。一个 GPG 帐号下可以有多个 uid,我可以使用根公钥签署类似于「jysperm@gmail.com 是我的邮箱地址」的签名,来将自己的多个身份关联到一起,上面的 3 个 uid 即我的 2 个邮箱地址和一个头像图片。
我还可以使用根公钥签署一个类似于「我授权 1D795875 为我的子密钥,可以代替我进行签名等操作」的消息来添加额外的子密钥,例如上面的三个 sub 就是三个不同功能的子密钥。就像这样,其实对于 GPG 帐号的管理操作都是通过用私钥签名消息来实现的。
还可以列出与我有关的签名:
~> gpg --list-sigs jysperm
pub 4096R/E466CF1E 2014-11-23 [expires: 2017-05-17]
uid Wang Ziting <jysperm@gmail.com>
sig C07CFB96 2016-05-04 paomian <qtang@leancloud.rocks>
sig 3 7CDC82A7 2015-05-11 Yeechan Lu <wz.bluesnow@gmail.com>
sig 3 E466CF1E 2016-05-17 Wang Ziting <jysperm@gmail.com>
sig E411E711 2016-06-02 keybase.io/librazy <librazy@keybase.io>
sig B0B002B8 2016-07-13 dennis (Dennis Zhuang) <killme2008@gmail.com>
这里看到除了我自己之外,还有其他四个人为我 jysperm@gmail.com 这个 uid 进行了签名,认可了 E466CF1E 这个公钥属于 Wang Ziting <jysperm@gmail.com> 这个人。对他人的签名也是可以区分不同的级别的,例如对于「在论坛上混了个脸属」和「每天都见面的同事」你可以给予不同级别的签名来更准确地表达信任关系
使用 GPG
前面我们介绍了 GPG 的信任模型和通讯簿,那么可以在哪些场景下使用 GPG 呢?
首先是你可以用它签名一段消息:
~> echo 'hello' | gpg --clearsign -a
-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA1
hello
-----BEGIN PGP SIGNATURE-----
iQIcBAEBAgAGBQJXfifAAAoJELQPOvDkZs8epZAP/3/jP6k1Dev2a8i8KfY7VDfv
TVGl61kLEbgpgR3mWXFL7PaJ8SyW8N0Dv3cJhYbY8NGp8wbkZa7cUS7DkTb2ArhS
M+IKUJtwUwbfp5fOyT+esaDLWatqjSJ+5IjWX8BOnh5SnLNMURDxsYrJMShfecTD
tbBfnEkIeCFBwIfE0Xs5m23+6i7t77ZgLdn1qpWLTRNpd6Fzi0B653Kr8dREPflI
MAsn6CP90pX55V0LnsZGiAgZV+34iFolhFDd7N5mtPT/zF7OToN2SNJF3YOVikBp
M+1WJL9W8x9DwzhOq8AmPgHIEwBZVNS8Nv+UNadIZJuexR0ERl64e8MdTLft0Qui
ChjUiD7ibkLR433jcms+2EJ04xd6Ie0mp/nH5nMLY1mEgHtLMXql6VHQCbJt80Vf
ZrL2J+BF9Sk1zPh9Hn5NGe+RLX1d/CZ62rYMICRcEwiS9vpWq6m9ouSMNZUYr8S5
a/ooD6gc71t457pVgkMqjo3Auazf4PRilUsAraQZilr+8yPhciE/PX3gBL5CtKHJ
4vKH9P9RngigL6D+YyBB5vMcpXlhx9ShbH2qLr106adJ1XrCpGtSmfxygjRn3xX9
Q1dWUaELUahhcdtK6IwZ6qzyp9AESpSd+Z/bnV7jc8iC0VtMOXipVnMo7J5qyHKD
/+yt8/tzoC4+0MEzlaHJ
=aOto
-----END PGP SIGNATURE-----
上面我们先用 SHA1 对要签名的文本进行进行了一下摘要,然后用 GPG 对这个摘要进行了签名。
因为 Git 中的用户名和邮件地址其实是可以随意更改的,之前有过几次伪造 Commit 冒充大 V 的事件发生。最近 GitHub 支持了为帐号配置 GPG 公钥,然后你便可以在发布新版本的时候用 git tag -s v1.0.0 进行签名:
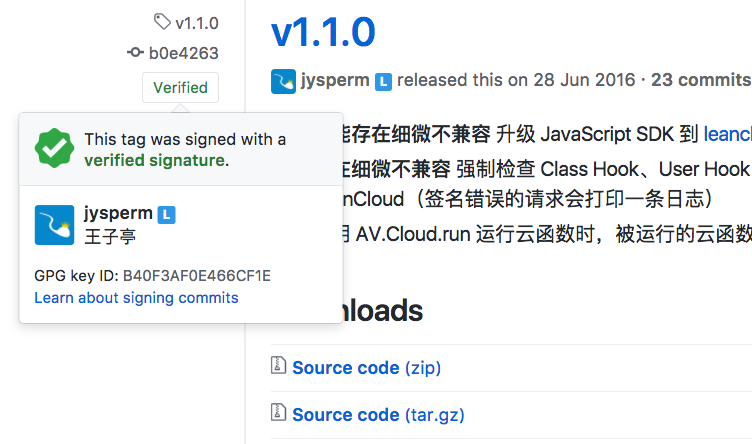
你可以在本地这样来验证签名,一旦签名认证通过,和正确的 GPG 帐号管理,那么这个 Commit 就不可能是伪造的:
~> git tag -v v1.1.0
object b0e42636df7394ac34f2b61c589233d0c3296d10
type commit
tag v1.1.0
tagger jysperm <jysperm@gmail.com> 1467084786 +0800
gpg: Signature made 6/28 11:33:17 2016 CST
gpg: using RSA key B40F3AF0E466CF1E
gpg: Good signature from "Wang Ziting <jysperm@gmail.com>"
很多开源软件在发布新版本的二进制包时也会使用 GPG 进行签名,包括 Debian 的软件仓库 apt 也是通过 GPG 进行签名的。
然后你当然也可以用 GPG 加密消息:
~> echo 'hello' | gpg --encrypt -a -r jysperm
-----BEGIN PGP MESSAGE-----
hQEMAyp325QokoazAQf8DDqELYisLFSGo/9Gblr1MEabb9t3V3AcbWkA4uimpYeD
/DTWDlmxrIsvpmDDeV/1bAZ/gMc2DzhODfM4PQf8DfD+lvHwgMBhe1zSBCZlQwkj
xkP+CtF+S8xWTciaexIMQiTHLNu1tvhvCjIeR1qYJY0/E7tdKhS5iG4Jc3/oyCNN
a1m34O9GG5WJsHozGqpfKZFma50onDmQ6TnSuz4iDWrslvq3XuLRXvgOQ6DKArix
Sxnmxg1kMvlIF6AMmQRHaHpyXBoOlaX/NEsl8ESCe9w4KZFTCoFtsEB9tAwQGeGn
6Tnd7BLaxXOabqaSpoNcOlpWDlZcX89lbewAryKbY9I7AbURsuemI37bTizQUjWA
57xm4t7wTUJ/FLx22Amv1ljUa/Rq84rO8d38EQViNGyo31UmRVXy12AmBDU=
=T42S
-----END PGP MESSAGE-----
这里我们指定了我自己的公钥为收信人,可以看到不同于前面,加密消息没有明文部分,除非使用收信人的私钥,否则无法解密:
$ gpg -d < gpg-message
gpg 2048-bit RSA key, ID 289286B3, created 2016-06-28 (main key ID E466CF1E)
Wang Ziting <jysperm@gmail.com>
hello
SSH
因为 SSH 和 GPG 都支持一样的公钥加密算法(例如 RSA),因此你也可以直接在 SSH 上使用 GPG 的密钥。
例如将你的 GPG 公钥添加到 GitHub,然后使用它来登录 GitHub:
~> export SSH_AUTH_SOCK=~/.gnupg/S.gpg-agent.ssh
~> ssh-add -l
2048 SHA256:wO93TcTQHZtltKfvS0jewFh0CMj4No6xnTegtB8FN+k
~> ssh git@github.com
Hi jysperm! You've successfully authenticated, but GitHub does not provide shell access.
Connection to github.com closed.
管理密码
有一个比较有趣的实践是你可以用 gpg 来加密你的密码,pass-store 是一个基于 GPG 和 Git 的非常简单的密码管理器,它可以用 GPG 来加密密码,然后用 Git 来进行版本控制:
~> pass find Coding
Search Terms: Coding
└── Code
└── Coding
└── jysperm.gpg
~> pass insert Code/Coding/jysperm
~> pass show Code/Coding/jysperm
DzizKKVIy22aHQwm
~> pass git pull --rebase
remote: Counting objects: 11, done.
remote: Total 11 (delta 1), reused 1 (delta 1), pack-reused 10
Unpacking objects: 100% (11/11), done.
From github.com:jysperm/passwords
5026f34..e94a70f master -> origin/master
First, rewinding head to replay your work on top of it...
Fast-forwarded master to e94a70f8b42af5e1c13dd69246b156bbcb24a94c.
这样一来你甚至可以把密码托管在 GitHub 上:https://github.com/jysperm/passwords
KeyBase 和身份证明

再向大家介绍一个有趣的社区 —— Keybase,它就好像是 GitHub 之于 GPG 社区一样。提供了一个你的 GPG 身份的主页,上面有你的公钥、关联的 GitHub 帐号、Twitter 帐号以及所拥有的网站,他人还可以在这个网页上直接用你的公钥发送经过 GPG 加密的信息。你可以将你的私钥以加密的方式存储在 Keybase(当然不推荐这样做),Keybase 提供了在浏览器中使用密钥对进行加密、解密、签名、验签的功能。
前面我们提到在 Keybase 上你可以关联你的社交帐号,不同于一般的网站的「第三方帐号关联」,Keybase 的用户们显然都对去中心化非常在乎,那么如何去证明一个社交帐号是属于这个 GPG 公钥的呢?在这个场景中我们需要进行两方面的证明,一方面是要用 GPG 公钥去进行一个签名,声明他拥有这个社交帐号:

另一方面是用这个社交帐号将这个签名发布出来,来声明他拥有这个 GPG 公钥:
这种交叉的证明将不同的数字身份联系到了一起,我觉得这是一个挺有趣的事情,于是我在 KeyBase 之外也自己创建了一个 GPG 主页,并在上面列出了一些和其他数字身份的交叉证明,例如邮件、V2EX 帐号等。我还注册了一个我的 GPG 公钥后八位的域名来指向这个页面:http://E466CF1E.pub
端到端加密
我们再来转向这篇文章的第二个话题「端到端加密」,下图中分别展示了在无加密、SSL 加密和端到端加密的场景下,从 A 到 B、中间经过服务器的一次通讯的过程:
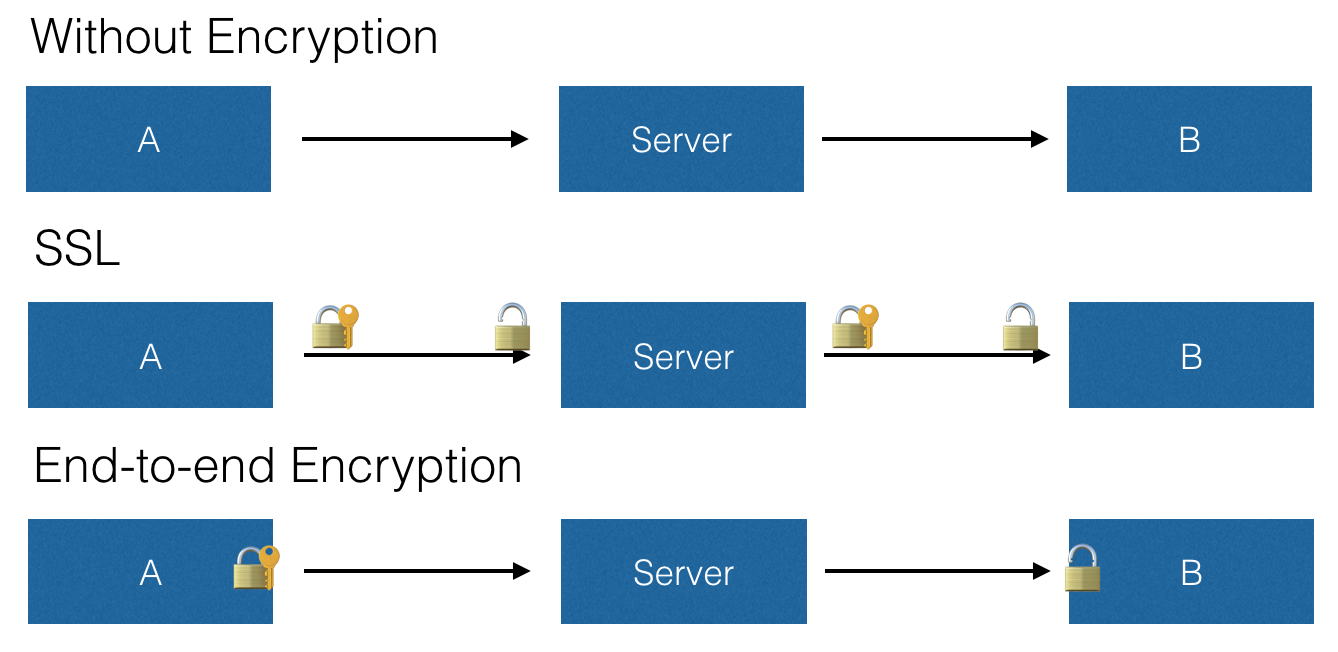
在没有加密的情况下,消息从 A 到服务器、再到 B 的全程都没有加密。这也意味着数据经过的链路上的任何一个节点(例如运营商的路由器)都可以查看和修改消息的内容,这种情况下的通讯安全是完全没有保证的。
在经过 SSL 加密的情况下,A 和 B 会分别在收发消息前通过 CA 签署的证书去认证服务器的身份,并协商一个用于加密数据的密钥。在从 A 到服务器,或从服务器到 B 的过程中,SSL 会保证数据不被窃听和篡改,但消息在服务器上则是以未加密的形态存在的,服务器可以查看和修改消息的内容,进行一些内容上的审查。
在端到端加密的情况下,消息在从 A 发出之前,就会利用我们前面介绍过的公钥加密技术,使用 B 的公钥进行加密,中间以加密的形式经过服务器和其他路由节点,直到 B 收到消息后,才使用自己的私钥进行解密。这种情况下的服务器并不能查看和修改消息,仅仅作为一个渠道来转发消息。
我们当然可以简单地使用 GPG 加密我们在第三方即时通讯软件上的聊天内容,就像下面这样:
但实际上例如 Tox、Line、WhatsApp、iMessage 等 IM 软件,都是默认提供了端到端加密的特性的,我们下面以 iMessage 为例去介绍一个 IM 软件是如何完成端到端加密通讯的。
iMessage 会在每台设备上生成一个 RSA 密钥对用于对数据进行加密,以及一个 ECDSA 密钥对用作签名(它出于安全性和性能的考虑使用了不同的密钥对,但其实是可以用同一个密钥对的)。这些密钥对中的公钥会被上传到 Apple IDS(Identity Services),然后其他用户会从 IDS 中取得你的所有公钥(每个设备一个公钥)。在 iMessage 中发出的所有文字消息都会使用自己的 ECDSA 私钥进行签名,使用对方的每个设备的 RSA 公钥加密一份,通过 APNs 发送给对方。对于多媒体消息,为了减少加密带来的开销,以及加密多份的流量开销,会使用一个临时密钥加密一次,通过 iCloud 进行传输,然后通过前面提到的方式发送临时密钥。苹果的很多应用都使用类似的方式进行端到端加密,包括 iCloud、Facetime、Keychain 等。
但在这个架构中,Apple IDS 依然是一个中心化的单点,它控制了全部的公钥交换过程,而且不允许用户干预。这就意味着 Apple 依然可以在 IDS 上进行中间人攻击,这也印证了我们在一开始提到的,公钥的交换是一个无法绕开的问题。在 GPG 中,用户需要繁琐地完全手动地去建立信任关系,换取了最高的去中心化程度;而在 iMessage 中 IDS 代劳了公钥交换的工作,方便了用户,但也引入了安全风险。
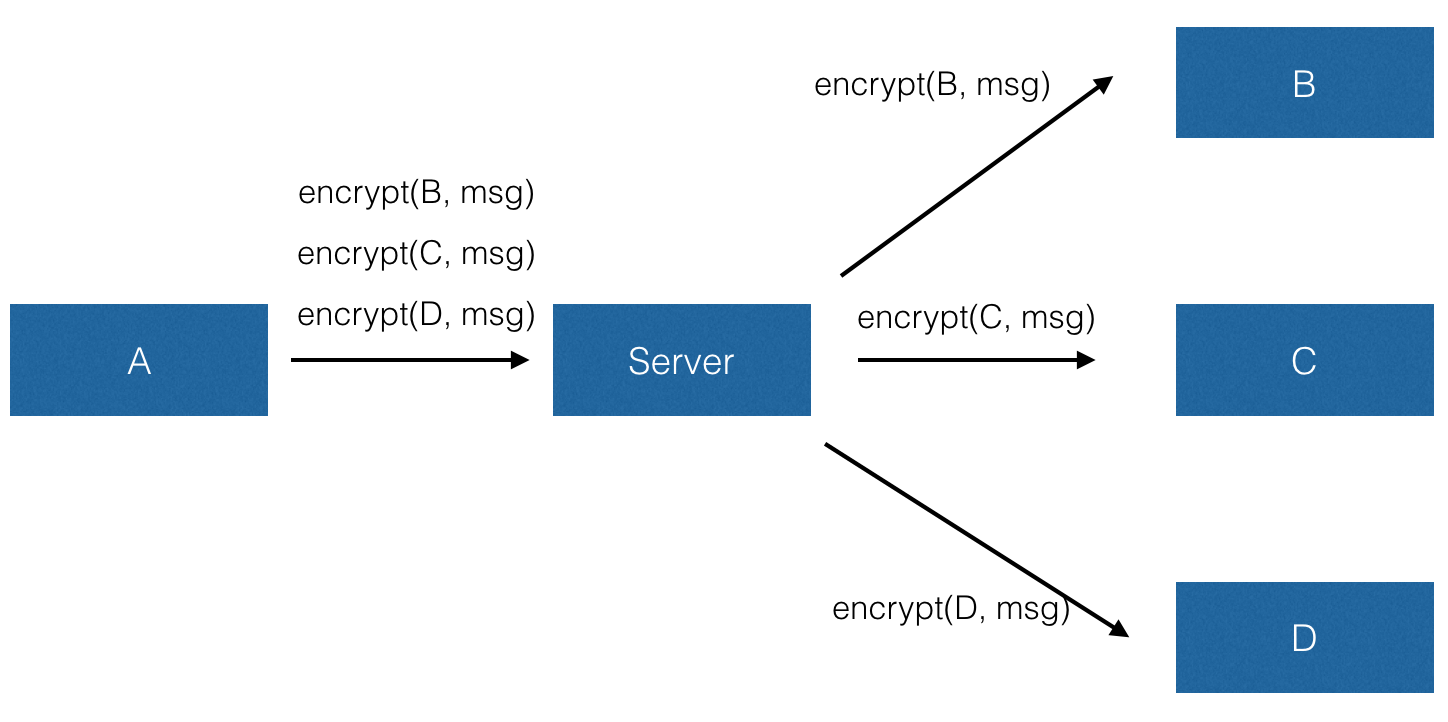
同时群聊也是一个比较难以解决的问题,在 Telegram 中群聊是无法开启端到端加密模式的,在 iMessage 中群聊也不总是可以使用端到端加密。这是因为就像前面提到的多设备的情况一样,在群聊的情况下我们必须用每个人的公钥来加密数据,这样数据在发送端就会膨胀许多倍(而不能发送端只发送一份,由服务器转发),具体的带宽开销会取决于群聊中的人数:
保管密钥
前面我们提到,在密码学账户中,你拥有一个账户的唯一凭证就是你的密钥对,一旦遗失,那么你便没有办法再去控制这个账户;或者一旦泄漏,其他人便拥有和你一样的控制这个账户的能力,无法重置,因此对密钥的保管显得尤为重要。
「备份」是具有两面性的 —— 一方面会让密钥更不容易丢失,但也让密钥变得更加容易泄漏。于是我就有个有趣的想法:能否做到将一个密钥分为若干「片段」保存,仅当拥有其中大部分片段的的时候才能够还原出密钥,但丢失了小部分片段又不影响还原呢?比如将密钥分为 5 份,仅当拥有其中任意三份的情况下可以还原出密钥。于是我找到了一个叫「Shamir’s Secret Sharing」的算法来做到这一点:
~> ssss-split -t 3 -n 5
Generating shares using a (3,5) scheme with dynamic security level.
Enter the secret, at most 128 ASCII characters: my secret root password
Using a 184 bit security level.
1-1c41ef496eccfbeba439714085df8437236298da8dd824
2-fbc74a03a50e14ab406c225afb5f45c40ae11976d2b665
3-fa1c3a9c6df8af0779c36de6c33f6e36e989d0e0b91309
4-468de7d6eb36674c9cf008c8e8fc8c566537ad6301eb9e
5-4756974923c0dce0a55f4774d09ca7a4865f64f56a4ee0
~> ssss-combine -t 3
Enter 3 shares separated by newlines:
Share [1/3]: 3-fa1c3a9c6df8af0779c36de6c33f6e36e989d0e0b91309
Share [2/3]: 5-4756974923c0dce0a55f4774d09ca7a4865f64f56a4ee0
Share [3/3]: 2-fbc74a03a50e14ab406c225afb5f45c40ae11976d2b665
Resulting secret: my secret root password
但将密钥作为一个文件,尤其是未加密的文件存储在电脑上仍然还是相当不安全的,因为你的电脑上安装了太多乱七八糟的软件了,目前大多数桌面操作系统其实都没有很好的权限控制 —— 几乎所有软件都可以随意地读取你所有的文件。因此 存储在硬盘上的文件是早晚要泄漏的,我们应该把密钥存储到一个无法被读取的地方,这就是我们下面要介绍的 TPM 芯片。

作为一个芯片来讲,外界必须通过已经被硬件定义好的协议去操作它,而对于 TPM 来讲,它在硬件的设计上就不允许你从芯片中取出私钥,你只能将私钥存进去,或者在 TPM 上生成密钥对。之后和私钥有关的所有运算,包括解密和签名都是在 TPM 芯片上进行的,整个过程中密钥都不会离开 TPM 芯片,即使作为硬件的 TPM 芯片被盗,他人也无法复制芯片中的私钥。
TPM 其实存在与很多笔记本和手机中,iPhone 的存储芯片和指纹识别都是依赖于 TPM 工作的。我目前在使用是的一款叫 Yubikey 的 USB TPM 芯片,它支持 GPG SmartCard 的标准,可以将 GPG 的密钥存储在其中。
小结
- GPG 可以在互联网上,以数学为基础创造一个无法被伪造的身份,并以此身份签名信息、接收加密信息。
- GPG 使用去中心化的信任模型,需要自行通过多种渠道来交换公钥,因此不会受制于单一的权威机构。
- GPG 提供了身份管理和相互进行「信任签名」的机制来简化密钥的交换过程。
- GPG 是一个开放的标准(兼容很多软件和硬件),有着活跃的社区,提供了相对易用的工具来进行公钥加密、解密、签名、验签。
- 基于公钥加密并签名的端到端加密是从理论上保证通讯安全的唯一方法,但在此之前你需要通过某种方式来交换公钥。
- 如果私钥丢失就只能改头换面、重新做人了。